接雨水 && 盛最多水的容器——动态规划&双指针

# 接雨水

题目就是给一个高度的一维数组，说实话这个题目如果不看答案感觉很难想到解法，我倒是想到了要记录每格的状态，其他的完全想不到怎么接着写了。

![image.png](https://www.snowkagura.com/usr/uploads/2025/07/2990057955.png)

后续看了答案才恍然大悟，最关键的要素就是知道每格的左右最大高度，其中最小的和这一格的当前高度的差就是这一格能存的水量，即如下公式：$min(leftMax, rightMax) - height[i]$

那么leftMax和rightMax怎么获得，最简单的想法就是从左到右、从右到左分别遍历一遍就可以得到了。

也就是下面这种解法：

```go
func trap(height []int) int {
    n := len(height)
    leftMax := make([]int, n)
    rightMax := make([]int, n)
    leftMax[0] = height[0]
    for i := 1; i < n; i++ {
        leftMax[i] = max(leftMax[i-1], height[i])
    }
    rightMax[n-1] = height[n-1]
    for i := n - 2; i >= 0; i-- {
        rightMax[i] = max(rightMax[i+1], height[i])
    }
    res := 0
    for i := 0; i < n; i++ {
        res += min(leftMax[i], rightMax[i]) - height[i]
    }
    return res
}
```

接着我们来思考这里还有没有优化的空间，经过上面的解法我们能得到一个结论：

**一个位置能接多少水，完全取决于它左边最高的墙和右边最高的墙中较矮的那一方。**

如果我们用两个指针分别指向最左和最右边，然后逐渐向中间靠拢，不断更新当前左边的最大高度和右边的最大高度呢？

假设这个时候的 `height[left] < height[right]`，那么左边的这根柱子肯定更短（思考一下，当前这个地方的高度都小于右边的高度了，那右边最高值只会大于等于这个高度，所以 `leftMax` 肯定会比较短，这里要记住指针一次只会移动一侧，按照这个思路去进行模拟，你一定能理解这里为什么能保证），也就满足了它**左边最高的墙较矮**这个条件，那么如果 `leftMax > height[left]`这里就必然会存储雨水；反之，如果 `height[left] >= height[right]`，右边的这根柱子就更短，这个时候如果 `rightMax > height[right]`，这里也必然会存储雨水，所以我们可以把逻辑简化如下：

```go
func trap(height []int) int {
    n := len(height)
    res := 0
    left, right := 0, n-1
    leftMax, rightMax := height[left], height[right]
    for left < right {
        if height[left] < height[right] {
            if leftMax < height[left] {
                leftMax = height[left]
            } else {
                res += leftMax - height[left]
            }
            left++
        } else {
            if rightMax < height[right] {
                rightMax = height[right]
            } else {
                res += rightMax - height[right]
            }
            right--
        }
    }
    return res
}
```

# 盛最多水的容器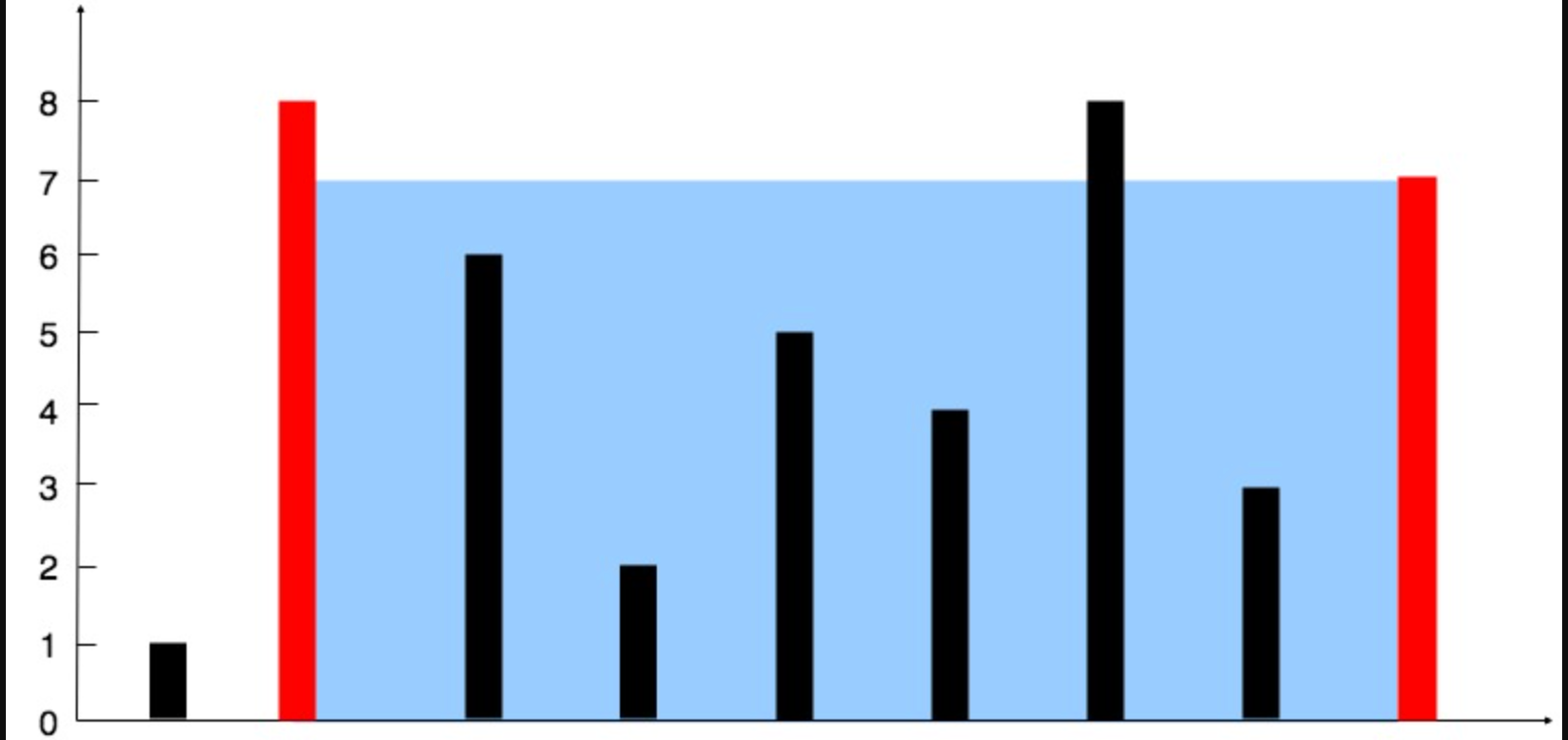

![image.png](https://www.snowkagura.com/usr/uploads/2025/07/1800052004.png)

这道题类似于接雨水，但是需要求的东西不同，这里要求盛水最大的容器，原理上来说可以暴力求解，但是会有测试用例过不了，时间限制超出，想要过就必须优化成 O(n)，也就是类似接雨水的双指针来做，甚至解法都差不多，每次遍历柱子低的收缩，然后求解对应的面积即可。

```go
func maxArea(height []int) int {
    n := len(height)
    res := 0
    i, j := 0, n-1
    for i < j {
        res = max(res, min(height[i], height[j]) * (j - i))
        if height[i] < height[j] {
            i++
        } else {
            j--
        }
    }
    return res
}
```

Last modification：July 13, 2025